Number System
Educator
Lav Goyanka,
India
|
Category
Academics & Technical - Academics - Maths
Explore the number system: natural, integers, rationals, irrationals, nth roots, rationalization, and laws of exponents. Join us!
-
Level
-
3x per week
-
500 students
By the end of this course, students will be able to:
- Represent natural numbers, integers, and rational numbers on the number line accurately and confidently.
- Differentiate between terminating and recurring decimals, and understand their connection to rational numbers.
- Perform operations on real numbers, including addition, subtraction, multiplication, and division.
- Identify non-terminating and non-recurring decimals and understand the concept and existence of irrational numbers (like √2, √3, π).
- Represent irrational numbers on the number line and explain how every real number corresponds to a unique point on the line, and vice versa.
- Understand and define the nth root of a real number, and interpret its meaning both algebraically and geometrically.
- Learn and apply the concept of rationalization of denominators involving irrational numbers (like √x, √y, a ± √b), and simplify such expressions.
- Recall and apply laws of exponents with integral powers, and gradually extend understanding to rational exponents with positive real bases through specific examples.
- Build a strong conceptual foundation in the structure of the real number system and its operations, enabling a better understanding of algebraic expressions and higher-level math.
Curriculum Overview
- Review of the representation of natural numbers, integers, and rational numbers on the number
line. Rational numbers as recurring/ terminating decimals. Operations on real numbers. - Examples of non-recurring/non-terminating decimals. Existence of non-rational numbers
(irrational numbers) such as , and their representation on the number line. Explaining
that every real number is represented by a unique point on the number line and conversely,
viz. every point on the number line represents a unique real number. - Definition of nth root of a real number.
- Rationalization (with precise meaning) of real numbers
and (and their combinations) where x and y are natural numbers and a and b are
integers. - Recall of laws of exponents with integral powers. Rational exponents with positive real bases
(to be done by particular cases, allowing the learner to arrive at the general laws.)
About the Educator | Credentials 
Gig Reviews
There are no reviews to display, yet.
-
Online Classes (Group) -
15 hr 30 min
-
3x per week
-
Age -
11to18+ yrs
-
Language -
English, Hindi
INR
1000.00
Weekly
More Gigs Like This
Goyanka
Number System
- All Levels
- 15 hours 30 minutes
- Age 11-18 yrs
-
INR 1000.00 per session
Goyanka
Rationalisation
- All Levels
- 4 hours 30 minutes
- Age 11-18 yrs
-
INR 2000.00 per session
Goyanka
Exponents Of Real Numbers
- All Levels
- 6 hours 30 minutes
- Age 6-18 yrs
-
INR 2000.00 per session
Lapsiwala
Rational Numbers
- All Levels
- 25 hours
- Age 6-15 yrs
-
INR 2500.00 per session
Oparachukwu
Basic Operations
- All Levels
- 16 hours
- Age 1-15 yrs
-
INR 2253.84 per session
B
Algebra 1: Your Path to Math Confidence
- All Levels
- 24 hours
- Age 11-15 yrs
-
INR 48000.00 per session
McKinney
Fabulous Fractions Multiplication!
- All Levels
- 8 hours
- Age 6-15 yrs
-
INR 150.00 per session
Shah
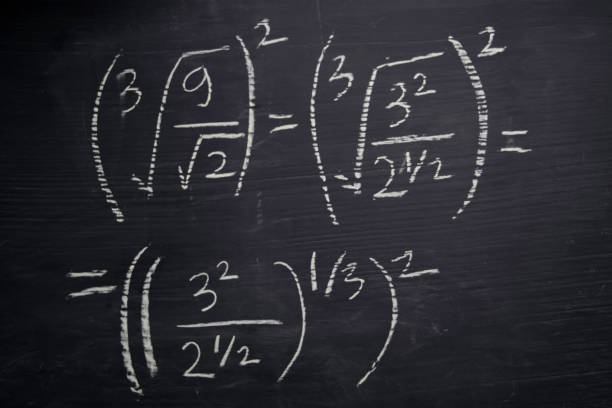
Academics
Tech Skills
Soft Skills
